
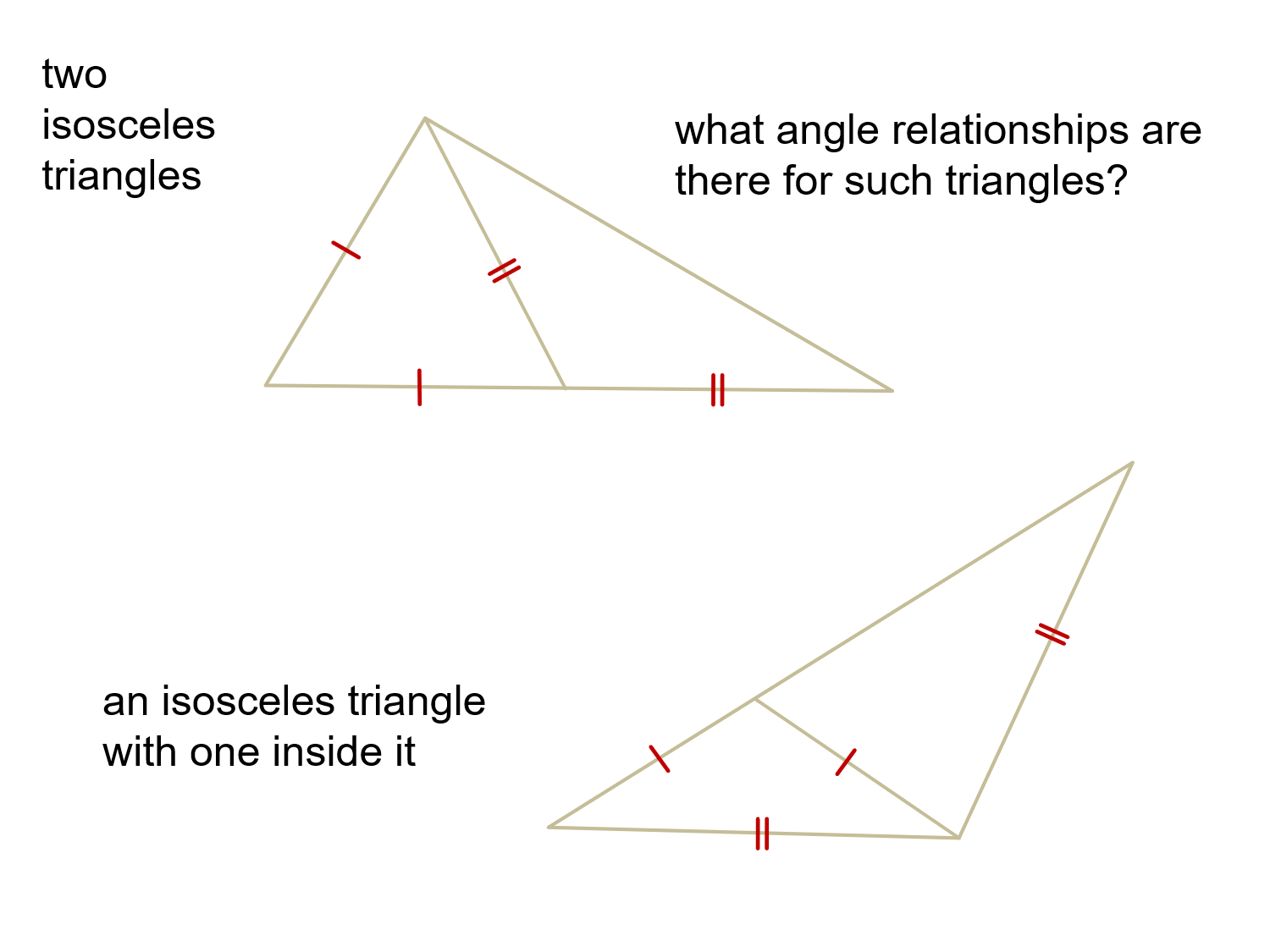
Formulas Height įor any isosceles triangle, the following six line segments coincide: These include the Calabi triangle (a triangle with three congruent inscribed squares), the golden triangle and golden gnomon (two isosceles triangles whose sides and base are in the golden ratio), the 80-80-20 triangle appearing in the Langley's Adventitious Angles puzzle, and the 30-30-120 triangle of the triakis triangular tiling.įive Catalan solids, the triakis tetrahedron, triakis octahedron, tetrakis hexahedron, pentakis dodecahedron, and triakis icosahedron, each have isosceles-triangle faces, as do infinitely many pyramids and bipyramids. Īs well as the isosceles right triangle, several other specific shapes of isosceles triangles have been studied. In Edwin Abbott's book Flatland, this classification of shapes was used as a satire of social hierarchy: isosceles triangles represented the working class, with acute isosceles triangles higher in the hierarchy than right or obtuse isosceles triangles. Since a triangle is obtuse or right if and only if one of its angles is obtuse or right, respectively, an isosceles triangle is obtuse, right or acute if and only if its apex angle is respectively obtuse, right or acute. In Euclidean geometry, the base angles can not be obtuse (greater than 90°) or right (equal to 90°) because their measures would sum to at least 180°, the total of all angles in any Euclidean triangle. Whether an isosceles triangle is acute, right or obtuse depends only on the angle at its apex. In the equilateral triangle case, since all sides are equal, any side can be called the base. The vertex opposite the base is called the apex.

The angle included by the legs is called the vertex angle and the angles that have the base as one of their sides are called the base angles. In an isosceles triangle that has exactly two equal sides, the equal sides are called legs and the third side is called the base. The same word is used, for instance, for isosceles trapezoids, trapezoids with two equal sides, and for isosceles sets, sets of points every three of which form an isosceles triangle. "Isosceles" is made from the Greek roots "isos" (equal) and "skelos" (leg). A triangle that is not isosceles (having three unequal sides) is called scalene. The difference between these two definitions is that the modern version makes equilateral triangles (with three equal sides) a special case of isosceles triangles. Terminology, classification, and examples Įuclid defined an isosceles triangle as a triangle with exactly two equal sides, but modern treatments prefer to define isosceles triangles as having at least two equal sides. 3 Isosceles subdivision of other shapes.1 Terminology, classification, and examples.The two angles opposite the legs are equal and are always acute, so the classification of the triangle as acute, right, or obtuse depends only on the angle between its two legs. The other dimensions of the triangle, such as its height, area, and perimeter, can be calculated by simple formulas from the lengths of the legs and base.Įvery isosceles triangle has an axis of symmetry along the perpendicular bisector of its base. The two equal sides are called the legs and the third side is called the base of the triangle. Isosceles triangles have been used as decoration from even earlier times, and appear frequently in architecture and design, for instance in the pediments and gables of buildings. The mathematical study of isosceles triangles dates back to ancient Egyptian mathematics and Babylonian mathematics.
Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case.Įxamples of isosceles triangles include the isosceles right triangle, the golden triangle, and the faces of bipyramids and certain Catalan solids. In geometry, an isosceles triangle ( / aɪ ˈ s ɒ s ə l iː z/) is a triangle that has at least two sides of equal length. Where h is the length of the hypotenuse and l is the length of the congruent sides.Isosceles triangle with vertical axis of symmetry In an isosceles right triangle, we know that the sides have congruent lengths, so we have the following formula: $latex p=h+l+l$ Therefore, we can calculate the perimeter of a triangle using the formula $latex p =a+b+c$, where, $latex a, ~ b, ~ c$ are the lengths of the sides. The perimeter is equal to the sum of the lengths of all the sides of the triangle. Where l is the length of one of the congruent sides of the triangle.

The area of any triangle can be calculated using the formula $latex A = \fracl \times l$


 0 kommentar(er)
0 kommentar(er)
